With less than a month left until the European championship and some free time, I built a simple simulation to predict the results of the tournament. You can find the whole code and run it yourself on Github. Its an ugly undocumented mess, yet it kinda works. Be warned!
I ran this simulation 1,000,000 times and wanted to share my results. There are some noticeable differences with the odds from sportsbooks, although nothing out of the ordinary.
The simulation
If you are not interested in how the simulation works, feel free skip all the boring bits and go directly to the results.
The idea is quite simple: create or use and existing model to predict the results of football games; stick the results of the games in the tournament and find out the winner. Repeat lots of times and find out the probability of each team winning the tournament.
Luckily, people already created ways to rank and predict results of two-players games. The most known one is the Elo rating system. Initially, It was intended as an improved chess rating system, but is also used as a rating system in lots of other games and sports. In fact, the match-making algorithm in most multiplayer games is based on the Elo system.
For national team football, there is an up to date Elo rating system available at eloratings.net. Thanks to Kirill (and any other people) for managing and updating it. I don’t know how good the prediction by this system are and it also a has couple of limitations, however for our unscientific, just for fun, experiment it is good enough.
Predicting draws
If you have a closer look at the Elo system you will notice that it does not give you the probability of each outcome (win, draw or loss). Instead it treats win as a point, draw as half-point and loss as nothing and return the expected result. In cases where draws are not allowed (e.g. playoff rounds), this value is the same as the win probability. However, for the group stage we need a way to predict draws as well.
David Dormagen from Free University of Berlin faced the same problem in 2014. Thankfully, he publish his solution to this problem in a section of “Development of a Simulator for the FIFA World Cup 2014”. So I am will use the same method, sumarised by this formula:
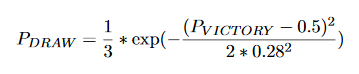
Tie-breaker
The Euro 2016 has comprehensive tiebreaker rules to make sure that teams are ordered by some skill-based property. The model we use predicts only the game outcome: win, draw or loss. It does not predict the final score. Adding draw-prediction already feels like taking the model beyond its capabilities, so I am not going to extend it any further. Instead our tiebreaker will consist of two rules:
- Higher number of points obtained;
Drawing of lotsA randomly generator number.
Reddit user gohuskies proposed an alternative method which is able to predict the final game scores as well. This method is based on the assumption that higher ranked teams score on average more goals and uses the Elo raking to predict the number of goals scored by each team in the game. This sounds like an interesting alternative approach to what i am using here.
France
Being the host, France have an automatic place in the tournament and did not play in the qualification round. As a result their rating variations for the last two years is based solely on friendly matches. Thus their rating might not be a true representation of their strength as some national teams use friendlies as a trial for new players and strategies.
They also get a 100 points boost for being the host nation which allows them to overtake Germany as the team with the highest rating.
Results
The table bellow shows the percentage of the teams reaching each round of the competition. The value are rounded to two non-zero digits, but shows the real value on hover.
You can sort the table based on any column, just by clicking on the header. This is done by the sortable library. You can also toggle red-green scaled coloring of the cells
You can also download the raw table in csv format and open it in Excel, LibreOffice Calc or other compatible software.
| Team | Elo | 4+ | 3+ | 2+ | 1st | 1/16 | 1/8 | 1/4 | Final | Win | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| France | 2047 | A | 1.0 | 0.985004 | 0.926749 | 0.746216 | 0.952993 | 0.774739 | 0.612210 | 0.407821 | 0.278695 |
| Germany | 2037 | C | 1.0 | 0.980305 | 0.902630 | 0.690674 | 0.937810 | 0.779634 | 0.572565 | 0.375420 | 0.250762 |
| Spain | 1977 | D | 1.0 | 0.935071 | 0.805860 | 0.563105 | 0.873594 | 0.647535 | 0.416696 | 0.265685 | 0.139537 |
| England | 1934 | B | 1.0 | 0.950894 | 0.838690 | 0.603733 | 0.895695 | 0.641500 | 0.383712 | 0.207418 | 0.096680 |
| Portugal | 1885 | F | 1.0 | 0.929710 | 0.789575 | 0.528687 | 0.863494 | 0.521821 | 0.268633 | 0.128776 | 0.051332 |
| Belgium | 1896 | E | 1.0 | 0.879272 | 0.689884 | 0.413902 | 0.796458 | 0.468432 | 0.242255 | 0.117500 | 0.050782 |
| Italy | 1844 | E | 1.0 | 0.821404 | 0.583775 | 0.292684 | 0.728002 | 0.374079 | 0.174660 | 0.074686 | 0.026124 |
| Ukraine | 1797 | C | 1.0 | 0.837086 | 0.523354 | 0.160413 | 0.727565 | 0.353468 | 0.153930 | 0.057359 | 0.016305 |
| Turkey | 1797 | D | 1.0 | 0.736112 | 0.446130 | 0.168860 | 0.639014 | 0.294287 | 0.121496 | 0.045218 | 0.013254 |
| Croatia | 1794 | D | 1.0 | 0.731955 | 0.440093 | 0.165836 | 0.635075 | 0.289824 | 0.118998 | 0.043727 | 0.012746 |
| Austria | 1766 | F | 1.0 | 0.815466 | 0.560995 | 0.245197 | 0.720611 | 0.317919 | 0.110981 | 0.036471 | 0.009730 |
| Poland | 1762 | C | 1.0 | 0.792649 | 0.436689 | 0.123085 | 0.676813 | 0.288182 | 0.113812 | 0.037730 | 0.009445 |
| Switzerland | 1753 | A | 1.0 | 0.798865 | 0.473614 | 0.119873 | 0.697749 | 0.286300 | 0.111156 | 0.036467 | 0.008500 |
| Russia | 1747 | B | 1.0 | 0.774350 | 0.486253 | 0.178624 | 0.677017 | 0.291799 | 0.094960 | 0.028001 | 0.007051 |
| Romania | 1738 | A | 1.0 | 0.777445 | 0.434642 | 0.106259 | 0.673352 | 0.260676 | 0.096251 | 0.030158 | 0.006543 |
| Ireland | 1751 | E | 1.0 | 0.666861 | 0.378780 | 0.154792 | 0.570381 | 0.215792 | 0.079554 | 0.025212 | 0.005894 |
| Sweden | 1735 | E | 1.0 | 0.632463 | 0.347561 | 0.138622 | 0.540088 | 0.192738 | 0.067656 | 0.020408 | 0.004538 |
| Slovakia | 1715 | B | 1.0 | 0.719799 | 0.410848 | 0.140172 | 0.621306 | 0.235524 | 0.068353 | 0.017892 | 0.004009 |
| Czech Republic | 1728 | D | 1.0 | 0.596862 | 0.307917 | 0.102199 | 0.511493 | 0.183821 | 0.061426 | 0.017769 | 0.003865 |
| Hungary | 1671 | F | 1.0 | 0.654336 | 0.347105 | 0.123371 | 0.558812 | 0.171308 | 0.042631 | 0.009772 | 0.001788 |
| Iceland | 1647 | F | 1.0 | 0.600488 | 0.302325 | 0.102745 | 0.511338 | 0.141583 | 0.032208 | 0.006823 | 0.001096 |
| Wales | 1638 | B | 1.0 | 0.554957 | 0.264209 | 0.077471 | 0.475025 | 0.129330 | 0.027976 | 0.005346 | 0.000862 |
| Albania | 1578 | A | 1.0 | 0.438686 | 0.164995 | 0.027652 | 0.380767 | 0.075887 | 0.014787 | 0.002438 | 0.000258 |
| Northern Ireland | 1578 | C | 1.0 | 0.389960 | 0.137327 | 0.025828 | 0.335548 | 0.063822 | 0.013094 | 0.001903 | 0.000204 |
Who should I bet on?
Whoever you want! This is just a simple simulation based on the Elo rankings. There is no guarantee that this model is right or even close to being right. There are probably many other models that will do a better job at predicting the results.
Anyway, if you are still looking for some numbers or “maths” to make you feel better about your choice, here are some: I took the best odds for winning the tournament from oddschecker.com and multiplied this by the probability of wining which gives the expected outcome of the bet.
Basically if the tournament is repeated thousands of times and you make the same £1 bet each time, this is how many pounds you will get back on average. Same as the previous one, this table is sortable and the numbers are rounded, but you can get the exact value on hover.
| Team | Winning probability | Best odd | Expected outcome |
|---|---|---|---|
| Ukraine | 0.016305 | 101.0 | 1.6468050 |
| Romania | 0.006543 | 251.0 | 1.6422930 |
| France | 0.278695 | 4.5 | 1.2541275 |
| Germany | 0.250762 | 5.0 | 1.2538100 |
| Portugal | 0.051332 | 23.0 | 1.1806360 |
| Turkey | 0.013254 | 81.0 | 1.0735740 |
| England | 0.096680 | 10.0 | 0.9668000 |
| Spain | 0.139537 | 6.5 | 0.9069905 |
| Ireland | 0.005894 | 151.0 | 0.8899940 |
| Hungary | 0.001788 | 401.0 | 0.7169880 |
| Belgium | 0.050782 | 12.0 | 0.6093840 |
| Slovakia | 0.004009 | 151.0 | 0.6053590 |
| Switzerland | 0.008500 | 67.0 | 0.5695000 |
| Russia | 0.007051 | 71.0 | 0.5006210 |
| Italy | 0.026124 | 19.0 | 0.4963560 |
| Czech Republic | 0.003865 | 126.0 | 0.4869900 |
| Poland | 0.009445 | 51.0 | 0.4816950 |
| Sweden | 0.004538 | 101.0 | 0.4583380 |
| Croatia | 0.012746 | 34.0 | 0.4333640 |
| Austria | 0.009730 | 41.0 | 0.3989300 |
| Iceland | 0.001096 | 126.0 | 0.1380960 |
| Albania | 0.000258 | 501.0 | 0.1292580 |
| Northern Ireland | 0.000204 | 501.0 | 0.1022040 |
| Wales | 0.000862 | 81.0 | 0.0698220 |
Looking at the British islands: Betting on Northern Ireland and Wales is a very bad deal.
The best outcome is for Ukraine with an expected profit of 65%. Its possible to do the same calculations for reaching any other round of the tournament (e.g. final, semi-finals, play-off rounds) and see if there is an even better bet.
The only other countries that makes sense to bet on are Romania, France, Germany, Portugal and Turkey. These teams together have over a 60% chance of winning the tournament, not bad options after all.
The betting companies most likely have more advanced models and you should not take anything from here seriously.
Just in case I said or will say something stupid in the future: this is my own personal blog. Everything I post here is my own thoughts and not those of my family, friends, colleagues, employer, parrot, chinchilla or anyone/anything else.
